Cs.Kádár Péter - XXI. századi Diszkónika, 22. Számok és számrendszerek
Néhány ezer éve tudjuk már, hogy számok nélkül elképzelhetetlen az élet. Magyar őseink kezdetben a hatos számrendszert használták, ám később áttértek a hetes számrendszerre. Ezt az időszakot őrzi néhány kifejezésünk: hétfejű sárkány, hétpecsétes titok, hetedhét ország. A 17. században aztán áttértek a tízes jellegű számrendszerre. Azért jellegű, mert a helyiértéket még nem használták. Az akkori számjegyek rovásírásúak voltak.
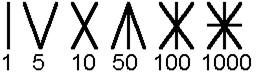

1 407-ből származik a legrégebbi hazai arab számjegyes feljegyzés.
A modern, hindu alapú, arabnak nevezett számrendszereket az alábbiak jellemzik:
- a számoknak van alaki és helyiértékük;
- létezik a nulla számjegy;
- léteznek a 0-nál kisebb ( negatív) számok is;
- a műveleteket és azok sorrendjét műveleti jelekkel és zárójelekkel ábrázolják;
- a műveletek végzésére és azok sorrendjére szabályok vannak;
- a 0-val való műveletvégzésnek külön szabályai vannak.
A számok alaki értéke azt mutatja meg, hogy a szám egy-egy elemi alkotórésze, a számjegy, hogyan néz ki.

A tízes számrendszerben 10 számjegy van: 0,1,2,3,4,5,6,7,8,9.
A számítástechnikában általánosan használt kettesben kettő: 0,1
A számítástechnikában megkülönböztetett szerepet játszó 8-as számrendszerben nyolc számjegynek kéne lennie: 0,1,2,3,4,5,6,7.
A számítástechnikában szintén megkülönböztetett 16-os számrendszerben pedig tizenhatnak: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.
A szánjegyek betűkkel történő alaki ábrázolása különben régi trükk, már a görögök is használták, de leszoktak róla.

A helyiérték azt mutatja meg, hogy a számrendszer alapjával – a tízes számrendszer esetén tízzel – hányszor kell megszorozni a számjegyet. Legyen mondjuk 318 a szám.
![]()
A sok nulla helyett a 10 fölé írt számmal – a hatványkitevővel – rövidebben is leírhatjuk ugyanezt. Főként, ha tudod, hogy minden szám nulladik hatványa egy.
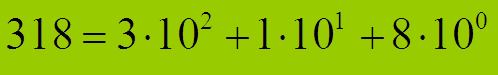 A hangtechnikában egyre gyakoribb, hogy egy jelet számmá, egy jelsorozatot számsorozattá alakítunk át. De mi ennek az előnye? Miért nem jó egy jel úgy, ahogy van?
A hangtechnikában egyre gyakoribb, hogy egy jelet számmá, egy jelsorozatot számsorozattá alakítunk át. De mi ennek az előnye? Miért nem jó egy jel úgy, ahogy van?
Megmondom az őszintét: bizony, nem jó. Hiszen minden átalakítás hibát okoz. Mégis van néhány igen nagy előnye, ha valamit számokkal jellemzünk. Ezek közül a legnagyobb, hogy a számokká alakított jeleket nagyon sokszor és alig romló minőségben lehet másolni, sokszorosítani. A Youtube videóján például azt láthatod és hallhatod, mi történik egy klippel, ha réges-régi kazettáról másolják újból és újból.
 A számokat azért könnyebb másolni, mert ki lehet egészíteni őket hibafelismerő és hibajavító újabb számjegyekkel.
A számokat azért könnyebb másolni, mert ki lehet egészíteni őket hibafelismerő és hibajavító újabb számjegyekkel.
Az egyik legegyszerűbb megoldás, ha a számot megismételjük: 318318. Ez nem túl elegáns, de gyakran használt eljárás. Például a merevlemezeken (vincsesztereken) háromszor is megismétlik a lemez tartalomjegyzékét.
Általában rövidebb számot kapunk, ha a számjegyeket összeadjuk, és ezt az új számot, az ellenőrző összeget, a szám után írjuk. 3+1+8=12, 31812 lesz az új szám.
Létezik azonban egy ennél is hatékonyabb módszer, a paritásos ellenőrzés. Ehhez ismerkedj meg a jobban a kettes számrendszerrel!
A kettes számrendszerben csak 1 és nulla fordulat elő, a helyiértékek a 2 hatványaival szerepelnek benne.
A kettes számrendszert Leibniz dolgozta ki még 1679-ben, majd 1854-ben George Boole alakította ki hozzá az algebrát. A Boole-féle algebrában nem csupán az összeadás és szorzás művelete lehetséges, hanem az ún. logikai műveletek is: és, vagy, negáció.
Ő itten Georg Boole

Az „és” azt jelenti, hogy egy állítás akkor igaz, ha mindkét (vagy több) feltétel egyszerre igaz: Akkor szerelmeskedhetsz Lujzával (Gézával), ha te is akarod és ő is akarja.
A „vagy” azt jelenti, hogy egy állítás akkor igaz, ha a két (vagy több) állítás közül legalább az egyik igaz: Akkor fogsz szeretkezni ma éjjel, ha vagy Lujza (Géza) vagy Gizi (Jenő) elmegy veled.
A „negáció” azt jelenti, hogy egy állítás ellenkezője igaz: Akkor vagy tisztességes, ha nemibetegként nem szeretkezel.
Nézzünk hát egy kettes számrendszerbeli számot!
![]() A kis szám jelöli, hogy milyen számrendszerről – esetünkben kettesről vagy tízesről – van-e szó. A két számrendszer között egyszerű az átváltás, de nehogy megerőltesd magad, a gépeden is van átváltó program, a tudományos számológépen. Számos átváltó automata van a neten is, például ez a villámgyors:
A kis szám jelöli, hogy milyen számrendszerről – esetünkben kettesről vagy tízesről – van-e szó. A két számrendszer között egyszerű az átváltás, de nehogy megerőltesd magad, a gépeden is van átváltó program, a tudományos számológépen. Számos átváltó automata van a neten is, például ez a villámgyors:
http://www.unitconversion.org/unit_converter/numbers.html
Ahogy beírod az egyik sorba a számjegyeket, máris írja az eredményt a másikban.
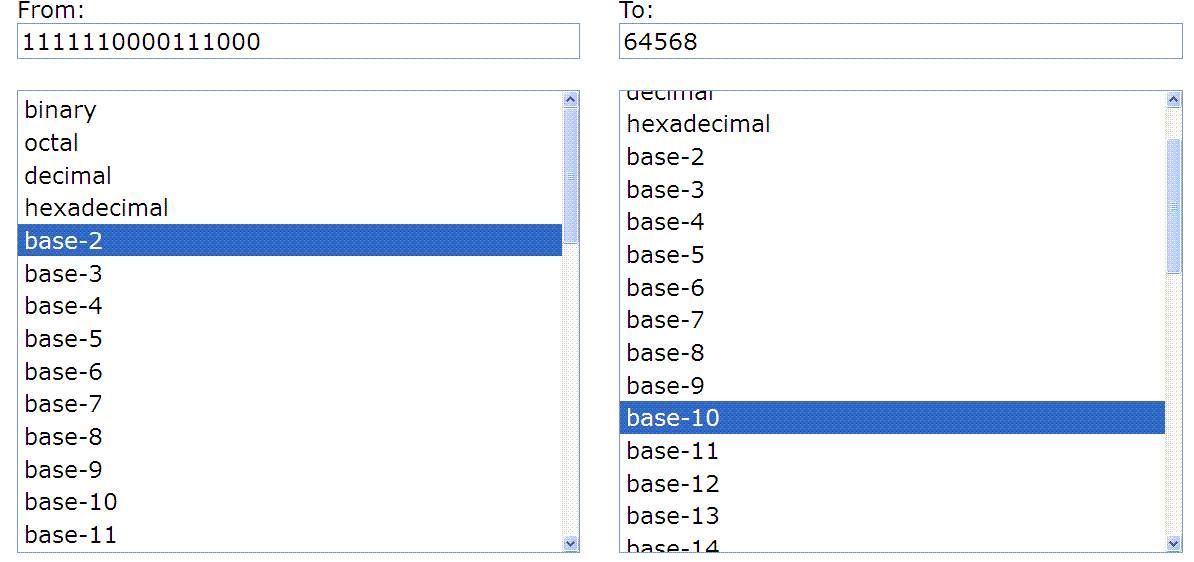
Tegyük föl, hogy az alábbi jelsorozatot kell továbbítani vagy rögzíteni:
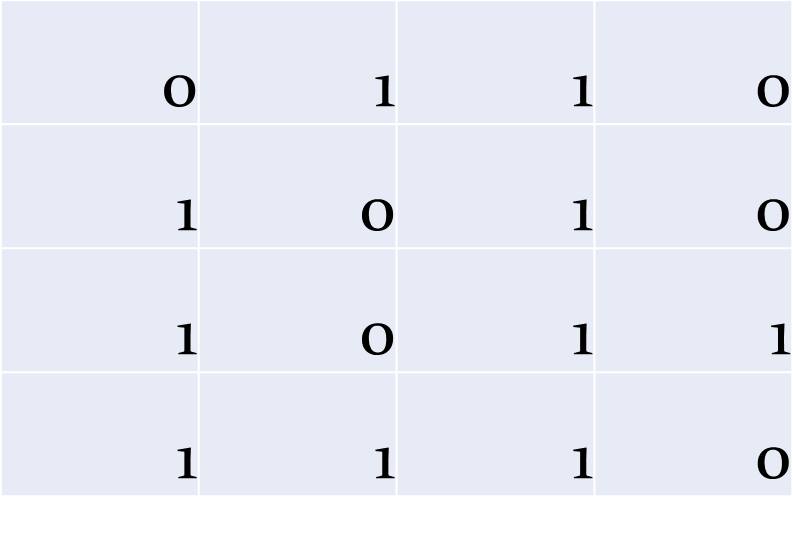
Helyette egy hibásat továbbított vagy rögzített a rendszer:
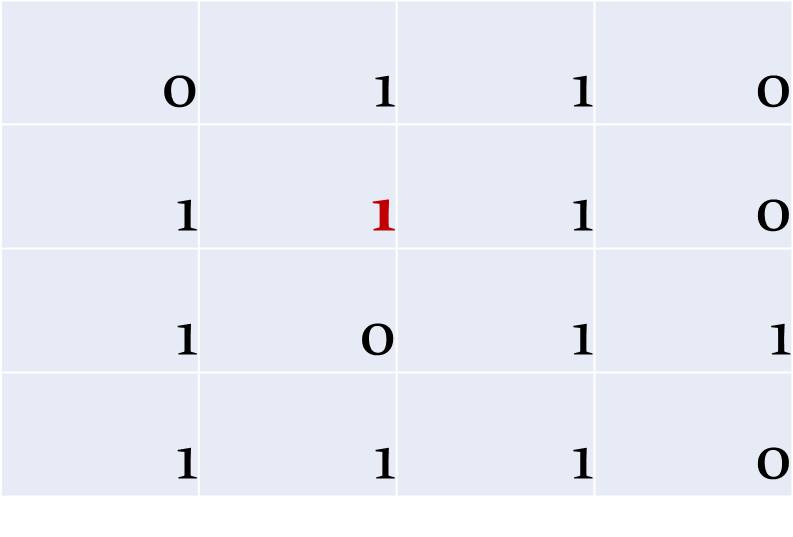
Az a cél, hogy megtalálja egy automata a hibát, és azt ki is javítsa. Először az eredeti jelsorozat minden sorához hozzá kell tenni egy számjegyet. Ha az eredeti sorban páros volt a számjegyek száma, akkor 0-t, ha páratlan, akkor 1-et. Vagyis minden sorban páros lesz az egyesek száma.
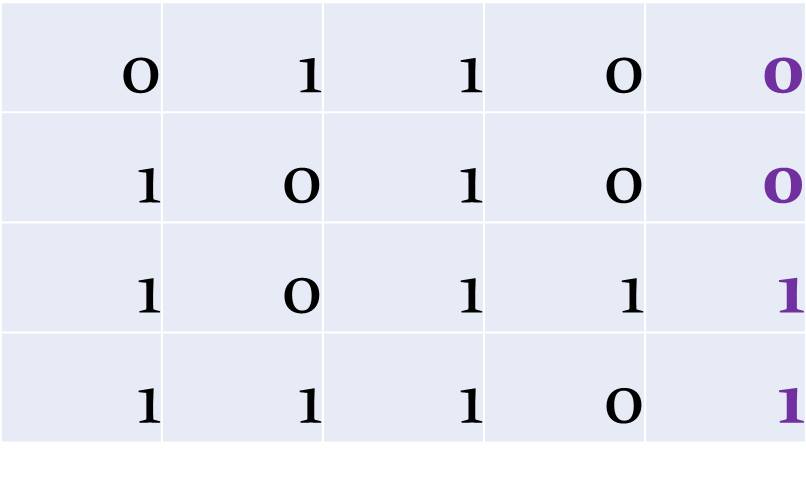
Az a sor hibás, amelyben páratlan az egyesek száma:
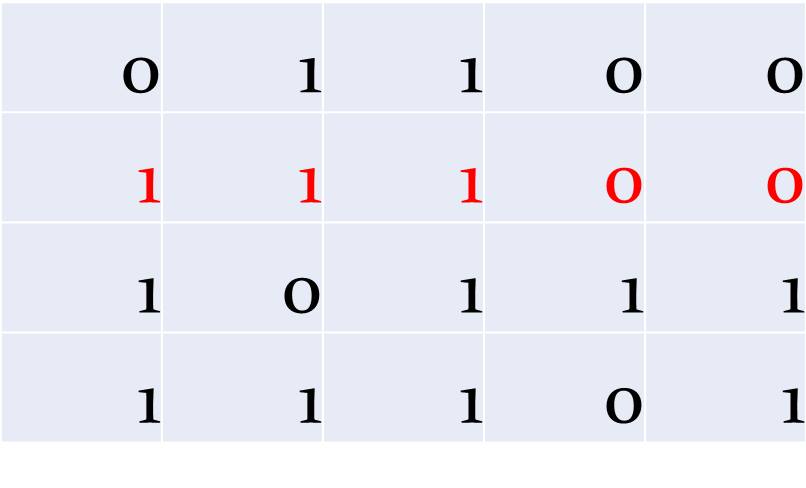
De még nem tudjuk, hogy melyik számjegy a hibás. Ezért az eredeti sorozat minden oszlopát is kiegészítjük úgy, hogy az egyesek száma minden oszlopban - a kiegészítő oszlopban is - páros legyen:
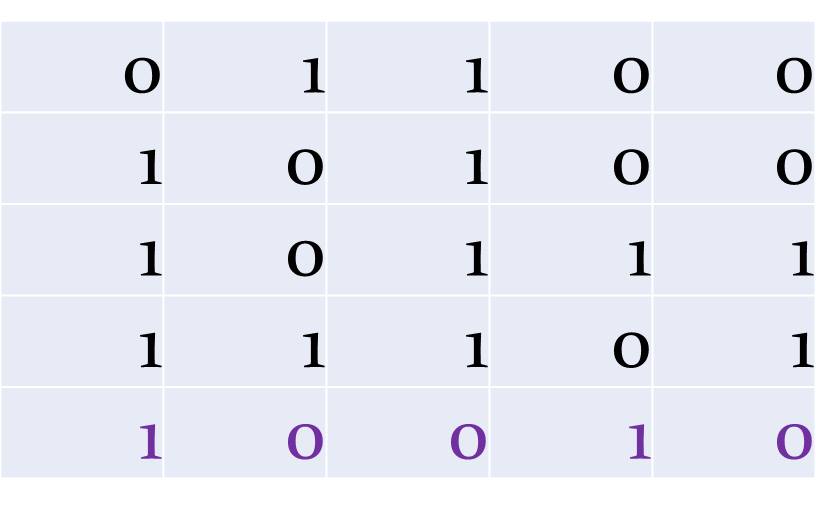
Az a hibás oszlop, amelyben az egyesek száma páratlan, és az a hibás sor, ahol az egyesek száma páratlan. A kettő metszéspontja a hibás bit, amit így egy automata ki is tud javítani, hiszen csak a hibás értéket kell kicserélni az ellenkezőjére.
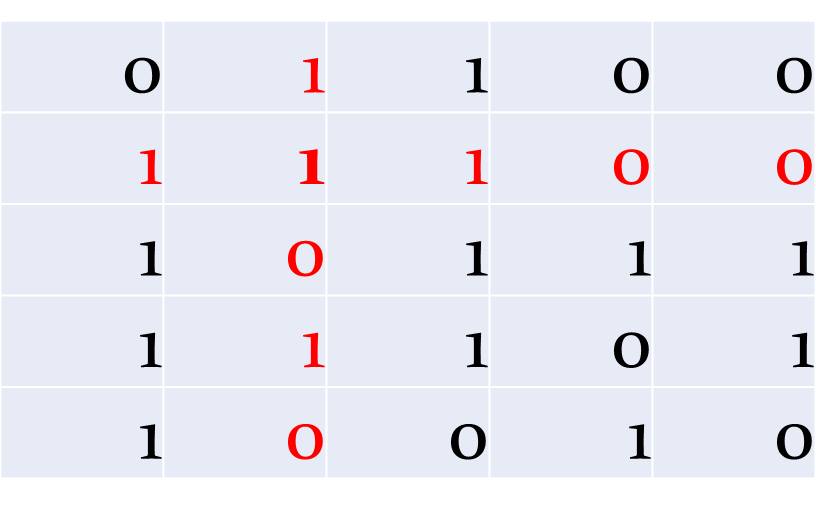
De mi van akkor, ha nem egy jegy a hibás, hanem kettő? Hiszen abban az esetben továbbra is páros maradhat az egyesek száma minden sorban és oszlopban, illetve, nem határozható meg két hibahely egyszerre. Meg lehet tenni például, hogy átlósan is paritás jegyeket képeznek, kiegészítik az összes sort és oszlopot az adott sor vagy oszlop összegével, aztán ismét paritásjegyeket képeznek, stb. Egy bonyolultabb rendszerben, pl. a hang-CD adatszerkezetében az adatoknak csak kb. a fele a hanginformáció, a másik fele lényegében hibafelismerő és javító kódokból áll. Ráadásul a lemezen az információk nem egymás után, hanem a lemez területén szétszórva helyezkednek el, mert annak valószínűsége, hogy egy karcolás az összes szétszórt elemet érje, nagyon csekély.
Az informatikában – mint már volt szó róla – a kettes számrendszerbeli szám egy jegyét – az egyest – az információ alapegysége, bitnek nevezik. 8 bitnyi információnak külön neve is van, ez a bájt. A kettőt nem szabad összekeverni, noha a nagy a kavarás. A bit jele b, a bájt jele B. A bájt miatt van jelentősége a nyolcas számrendszernek. Az informatikában azonban a nyolcas – más néven oktális –számrendszerbeli számokat kettes számrendszerbeli csoportokba írják át.
![]()
Ennek az az oka, hogy a számítástechnika csak két értéket használ, és mindent lebont erre a két értékre. Nincs ez másképp a 16-os számrendszerrel sem, csupán ebben az esetben nem három-, hanem négyjegyűek a számok.

A 16-os számrendszer előnye, hogy nagyon hajlékonyan használható. Olyannyira, hogy sokáig – az informatikában hosszú időnek számít már öt év is – olyan programokat írtak a számítógépre, amelyek 16 bitet használtak. Szinte minden gépre telepítették – valószínűleg véletlenül – a Strip Poker nevű cuccot.
A hangtechnikában 16 bites eszköz volt például az 1992-ben forgalomba hozott, Creative gyártmányú, Sound Blaster 16 elnevezésű hangkártya, ami sokáig iparági szabványnak számított.


